APLICACIÓN DE LA ESTADISTICA EJERCICIOS FISICOS

 LA ESTADISITCA 

CONCEPTO:

La Estadística es la parte de las Matemáticas que se encarga del estudio de una determinada característica en una población, recogiendo los datos, organizándolos en tablas, representándolos gráficamente y analizándolos para sacar conclusiones de dicha población.

Estadística descriptiva: Se refiere a los métodos de recolección, organización, resumen y presentación de un conjunto de datos. Se trata principalmente de describir las características fundamentales de los datos y para ellos se suelen utilizar indicadores, gráficos y tablas.

VARIABLES:

Una variable refiere, en una primer instancia, a cosas que son susceptibles de ser modificadas (de variar), de cambiar en función de algún motivo determinado o indeterminado.

El término variable alude a las cosas de poca estabilidad, que en poco tiempo pueden tener fuertes alteraciones o que nunca adquieren una constancia

Tipos de variables

Variable cuantitativa:

• Variable continua: Toman un valor infinito de valores entre un intervalo de datos. Ejemplo: el tiempo que tarda un corredor en completar los 100 metros lisos.

• Variable discreta: Toman un valor finito de valores entre un intervalo de datos. Ejemplo: Número de helados vendidos.

Variable cualitativa:

• Variable ordinal: Expresa diferentes niveles y orden. Por ejemplo, primero, segundo, tercero, etc.
• Variable nominal: Expresa un nombre claramente diferenciado. Por ejemplo el color de ojos puede ser azul, negro, castaño, verde, etc.

POBLACIÓN Y MUESTRA:

La población: 

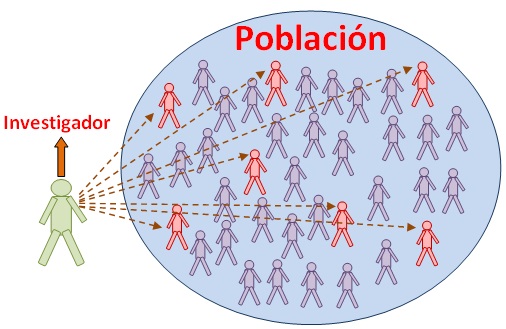
La población es el total de individuos o conjunto de ellos que presentan o podrían presentar el rasgo característico que se desea estudiar.

El vocablo suena a personas pero una población estadística puede estar constituida por cualquier tipo de elemento, es decir, una población puede estar constituida por personas pero también por objetos de cualquier tipo de naturaleza.

Tipos de variables:

• Población estadística finita: Es aquella en la que el número de valores que la componen tiene un fin. Por ejemplo, la población estadística que nos indica la cantidad de árboles de una ciudad es finita. Es cierto que puede variar con el tiempo, pero en un instante determinado es finita, tiene fin.
• Población estadística infinita: Se trata de aquella población que no tiene fin. Por ejemplo, el número de planetas que existen en el universo. Aunque puede que sea finito, el número es tan grande y desconocido que estadísticamente se asume como infinito.

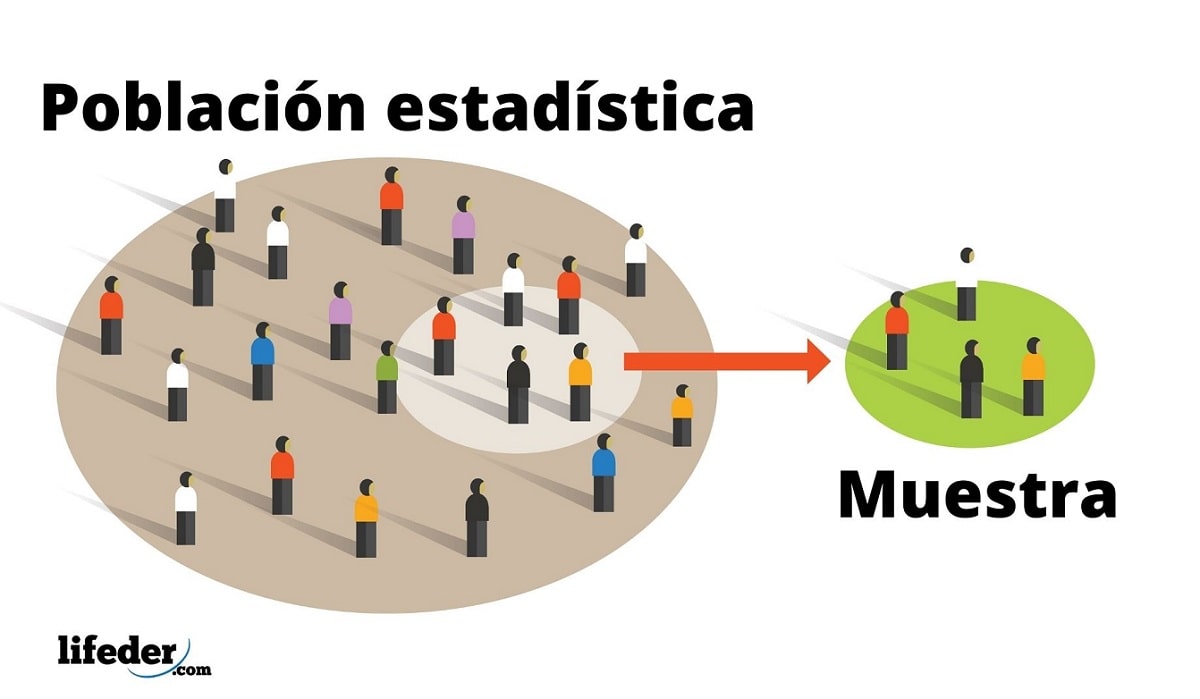
La muestra:

Cualquier subconjunto de una población. Cuando los elementos que componen la muestra están elegidos aleatoriamente y todos los elementos tienen la misma probabilidad de ser elegidos diremos que se trata de una muestra aleatoria simple.

Este método se utiliza cuando no se puede aplicar un censo en ciertas poblaciones, ya que a través del muestreo se puede establecer una porción de la realidad a estudiar.

Tipos de muestra estadística

El muestreo probabilístico:

es un método de muestreo (muestreo se refiere al estudio o el análisis de grupos pequeños de una población) que utiliza formas de métodos de selección aleatoria.

Dentro de la muestra probabilística podemos encontrar los siguientes tipos de muestreo:

• Muestreo aleatorio simple: método de selección más básico, en el que cada sujeto posee un número de identificación y, mediante un sorteo aleatorio, algunos son seleccionados para la muestra.

• Muestreo sistemático: con este método se enumera la población a trabajar y los investigadores se encargan de listar a cada individuo en grupos de 10, de forma aleatoria.

• Muestreo estratificado: consiste en dividir a la población en estratos o grupos que compartan características similares.

• Muestreo por conglomerados: se da cuando la población ya se encuentra dividida de forma natural en grupos, por lo que se seleccionan individuos aleatoriamente de cada conglomerado para conformar la muestra.

Muestra no probabilística:

El muestreo no probabilístico es una técnica de muestreo en la cual el investigador selecciona muestras basadas en un juicio subjetivo en lugar de hacer la selección al azar.


A su vez, este deriva en los siguientes tipos de muestreo:

• Muestreo por cuotas: los investigadores forman la muestra partiendo de determinadas características, con el fin de lograr la misma distribución de características en la muestra que en la población. Por ejemplo, si en una población hay 60% hombres y 20% mujeres, los individuos de la muestra deberán estar distribuidos de la misma manera.

• Muestreo por conveniencia: aquí el investigador suele elegir a los individuos de su muestra solo por su proximidad. Ejemplo cuando las empresas detienen a las personas en un centro comercial o en una calle concurrida para distribuir sus folletos promocionales y hacer preguntas.

• Muestreo por bola de nieve: se utiliza cuando el investigador requiere que un sujeto de su muestra ayude a identificar a otro con las mismas características y, a su vez, estos a otros, para formar la muestra deseada.

• Muestra discrecional: también conocida como muestreo por juicio o criterio, se da cuando el investigador selecciona los individuos de su muestra en base a determinado conocimiento de la población. Por ejemplo, si desea realizar una investigación de personas con problemas psicológicos en el embarazo, seleccionará aquellas mujeres que hayan pasado por la experiencia del embarazo.

MEDIDAS DE CENTRALIZACIÓN 

(CON DATOS AGRUPADOS)

DEFINICIÓN:

Son medidas estadísticas que pretenden resumir en un solo valor a un conjunto de valores. Representan un centro en torno al cual se encuentra ubicado el conjunto de los datos. 

Las medidas de tendencia central más utilizadas son: media, mediana y moda. Las medidas de dispersión en cambio miden el grado de dispersión de los valores de la variable. Dicho en otros términos las medidas de dispersión pretenden evaluar en qué medida los datos difieren entre sí.

MEDIA ARITMETRICA:

La medida de tendencia central más conocida y utilizada es la media aritmética o promedio aritmético. Se representa por la letra griega µ.

La media o también llamada promedio es la sumatoria de todos los valores de la variable dividida entre el numero de datos.

Formula:

En donde cada representa uno de nuestros datos y es el número total de datos que tenemos.

Ejemplo:

Es usado comunmente por ejemplo al momento de calcular promedio académico donde todas las calificaciones tienen el mismo peso, entonces el promedio es la suma de elementos dividido entre la cantidad de elementos.

MEDIANA:

Es el valor que ocupa el lugar central de todos los datos cuando éstos están ordenados de menor a mayor. 

La mediana se representa por Me. 

La mediana se puede hallar sólo para variables cuantitativas.

Formula: 

• es el límite inferior de la clase donde se encuentra la mediana
• es la semisuma de las frecuencias absolutas

• es la frecuencia absoluta de la clase mediana

• es la frecuencia acumulada anterior a la clase mediana

• es la amplitud de la clase

• La mediana es independiente de las amplitudes de los intervalos

Ejemplo:

Por ejemplo: si tenemos un grupo de notas académicas y queremos saber que valor corta los datos de manera que el 50% este por debajo del mismo y el otro 50% por encima entonces tomamos la mediana.

MODA:

La moda es el valor que tiene mayor frecuencia absoluta.

Se representa por Mo.

Cuando todas las puntuaciones de un grupo tienen la misma frecuencia, no hay moda. Se puede hallar la moda para variables cualitativas y cuantitativas

Formula:

• es el límite inferior de la clase modal
• es la frecuencia absoluta de la clase modal
• es la frecuencia absoluta inmediatamente inferior a la clase modal
• es la frecuencia absoluta inmediatamente posterior a la clase modal
• es la amplitud de la clase

Ejemplo:

• Por ejemplo en una tienda de ropa queremos saber que tipo de camisas se debe producir mas que las otras entonces vemos de las observaciones de camisas vendidas cual es la que mas se repite.
• Por ejemplo en una escuela saber que tipo de aperitivos que más se consume, es observando las que más se ve comiendo.